103. Binary Tree Zigzag Level Order Traversal
난이도: 중간 (Medium)
링크: LeetCode 103
풀이 날짜: 2025.10.10(다시품)
1. 문제 이해
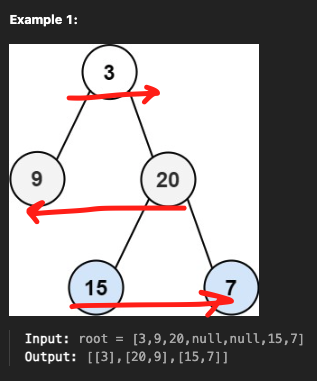
이진 트리의 각 레벨(level)을 좌 → 우, 우 → 좌 순서로 번갈아가며 순회한 결과를 2차원 배열로 반환하는 문제.
2. 접근 아이디어 및 자료구조
이 문제는 BFS (너비 우선 탐색) 으로 해결할 수 있는데,
각 레벨을 queue에 넣고 한 레벨씩 탐색하며,
방향을 나타내는 direction 변수를 사용해 순서를 제어하면 된다.
- direction = 1 → 왼쪽 → 오른쪽
- direction = -1 → 오른쪽 → 왼쪽
한 레벨이 끝날 때마다 direction *= -1로 방향을 반전시키는 것이 포인트.
3. 잘못된 접근 (초기 시도)
var zigzagLevelOrder = function(root) {
if(!root) return [];
const result = [];
const queue = [root];
let direction = 1;
while(queue.length > 0) {
const len = queue.length;
const group = [];
for(let i=0; i<len; i++) {
const node = queue.shift();
group.push(node?.val);
if(direction === 1) {
if(node.left) queue.push(node.left);
if(node.right) queue.push(node.right);
} else {
if(node.right) queue.push(node.right);
if(node.left) queue.push(node.left);
}
}
direction *= -1;
result.push(group);
}
return result;
};
처음에는 방향이 바뀌면 자식 노드를 넣는 순서도 바꾸는 방법이 정상 동작할 것이라 생각했으나,
이는 BFS 구조의 핵심을 놓친 접근이었다.
BFS에서 Queue의 동작방식
오해: “왼→오 방향일 땐 right부터, 오→왼 방향일 땐 left부터 넣으면 순서가 뒤집히겠지?”
현실:
1. BFS의 queue는 FIFO(First In, First Out)구조이다. 이론일 뿐만 아니라, 알고리즘 문제에서는 실제로 이렇게 동작한다! 즉, 넣는 순서를 바꿔도 꺼내는 순서가 바뀌지 않기 때문에 결과가 뒤집히지 않는 것이다.
2. “그럼 pop()으로 뒤에서 꺼내면 되지 않을까?” 라고 생각할 수 있지만, pop을 사용하면 스택(LIFO) 처럼 동작해서 DFS 탐색으로 바뀌게 되므로 순차적인 탐색이 불가능해진다.
4. 올바른 풀이 코드
var zigzagLevelOrder = function(root) {
if (!root) return [];
const result = [];
const queue = [root];
let direction = 1; // 1: 왼→오, -1: 오→왼
while (queue.length > 0) {
const len = queue.length;
const group = [];
for (let i = 0; i < len; i++) {
// BFS의 핵심은 "선입선출"
const node = queue.shift();
group.push(node.val);
// 다음 레벨 추가 (항상 left → right 순서)
if (node.left) queue.push(node.left);
if (node.right) queue.push(node.right);
}
// 방향이 오른쪽 → 왼쪽일 때만 뒤집기
if (direction === -1) group.reverse();
result.push(group);
direction *= -1;
}
return result;
};
꺼내는 동작은 큐의 특성(선입선출)에 맞게 queue.shift() 를 이용하여 가장 먼저 들어간 순서대로,
그리고 결과 배열에는 방향에 따라 배열을 뒤집어 넣어준다.
| 구분 | 복잡도 | 설명 |
| 시간 복잡도 | O(n) | 모든 노드를 한 번씩 방문 |
| 공간 복잡도 | O(n) | queue 및 결과 배열 저장 공간 |
5. 정리
| 포인트 | 설명 |
| 탐색 구조 | BFS (Queue, FIFO) |
| 순서 제어 | direction + group.reverse() |
| 잘못된 접근 | push 순서를 바꿔도 큐는 FIFO라 순서 안 바뀜 |
이 문제의 핵심은 “탐색 순서는 그대로 두되, 출력 순서만 바꾼다”.
여기서 출력 순서라 함은 탐색된 노드들을 결과 배열에 추가하는 순서를 말한다.
즉, 트리 탐색 로직은 평범한 BFS지만 결과를 가공하는 방식에서 지그재그 형태를 만들어내는 것이 이 문제의 포인트!