57. Insert Interval

난이도: 중간 (Medium)

링크: LeetCode 57

풀이 날짜: 2025/10/21

 

1. 문제 이해

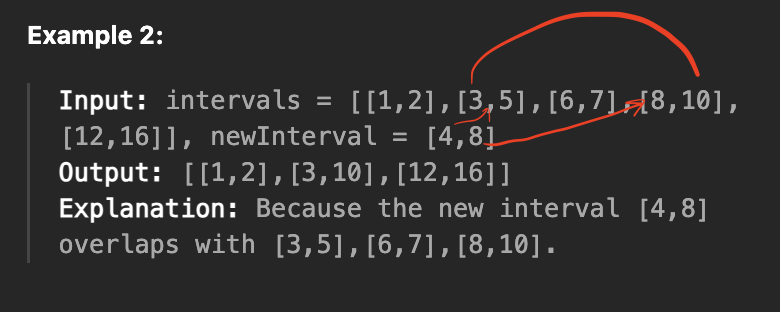
이미 정렬된 구간 배열 intervals가 주어지고, 새로운 구간 newInterval을 삽입하면서 겹치는 구간은 병합하여 최종 배열을 반환하는 문제이다.

 

 

2. 접근 방식 — 단계별 처리

핵심 아이디어: 세 구간으로 나누어 처리

1. newInterval보다 앞쪽에 겹치지 않는 구간 → 그대로 결과에 push
2. newInterval과 겹치는 구간 → 시작값은 min, 끝값은 max로 병합
3. newInterval 이후 뒤쪽 구간 → 그대로 결과에 push

이렇게 하면 한 번의 순회로 모든 조건을 처리가 가능하다.

 

3. 풀이 코드

/**
 * @param {number[][]} intervals
 * @param {number[]} newInterval
 * @return {number[][]}
 */
var insert = function(intervals, newInterval) {  
  const n = intervals.length;
  const result = [];
  let i = 0;

  // 1. newInterval보다 앞쪽에 겹치지 않는 구간
  while (i < n && intervals[i][1] < newInterval[0]) {
    result.push(intervals[i]);
    i++;
  }

  // 2. newInterval과 겹치는 구간
  // newInterval 의 end 값이 왼쪽 끝에 위치해도 intervals[i] 의 시작값과 같거나 크면 겹치는 것.
  while (i < n && intervals[i][0] <= newInterval[1]) {
    newInterval[0] = Math.min(newInterval[0], intervals[i][0]);
    newInterval[1] = Math.max(newInterval[1], intervals[i][1]);
    i++;
  }

  // 병합된 newInterval 추가
  result.push(newInterval);

  // 3. newInterval 뒤쪽 구간
  while (i < n) {
    result.push(intervals[i]);
    i++;
  }

  return result;
};

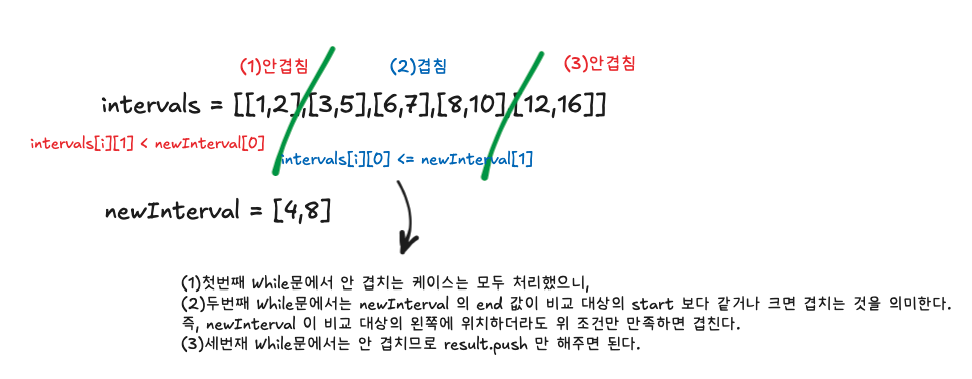
intervals가 이미 시작값 기준으로 정렬되어 있으므로, 순차적으로 한 번만 순회해도 병합 구간을 쉽게 찾을 수 있다. newInterval보다 앞쪽, 겹치는 구간, 뒤쪽으로 나누어 처리하면 반복과 조건문을 최소화가 가능하다.

 

겹침 조건은 intervals[i][0] <= newInterval[1]인데, 이걸 아래와 같이 생각해보자.

1. 두 구간을 시간축에 놓고 생각
   • intervals[i] = [a, b]
   • newInterval = [c, d]
   • 겹친다는 의미는 어떤 순간이라도 두 구간이 겹치는 시간이 있다는 것
2. 겹침 판단 기준
   • intervals[i][0] <= newInterval[1] → 현재 구간 시작점이 새 구간 끝보다 앞서거나 같으면, 겹칠 가능성이 있음.
   • 겹치면 새 구간을 newInterval[0] = min(a, c), newInterval[1] = max(b, d) 로 확장합니다.

즉, 새 구간 끝점보다 먼저 시작하는 구간은 겹칠 수 있다고 보는 것이 직관적 이해 포인트이다.

 

예시 시나리오

입력:

intervals = [[1,2],[3,5],[6,7],[8,10],[12,16]], newInterval = [4,8]

단계	i	newInterval	result	설명
1	0	[4,8]	[[1,2]]	intervals[0]=[1,2]는 newInterval과 겹치지 않음 → 결과에 push
2	1	[4,8]	[[1,2]]	intervals[1]=[3,5]와 겹침 → 병합: newInterval=[3,8]
3	2	[3,8]	[[1,2]]	intervals[2]=[6,7]와 겹침 → 병합: newInterval=[3,8]
4	3	[3,8]	[[1,2]]	intervals[3]=[8,10]와 겹침 → 병합: newInterval=[3,10]
5	4	[3,10]	[[1,2],[3,10]]	병합 완료 후 newInterval push
6	4	[3,10]	[[1,2],[3,10],[12,16]]	나머지 구간 intervals[4]=[12,16] 추가

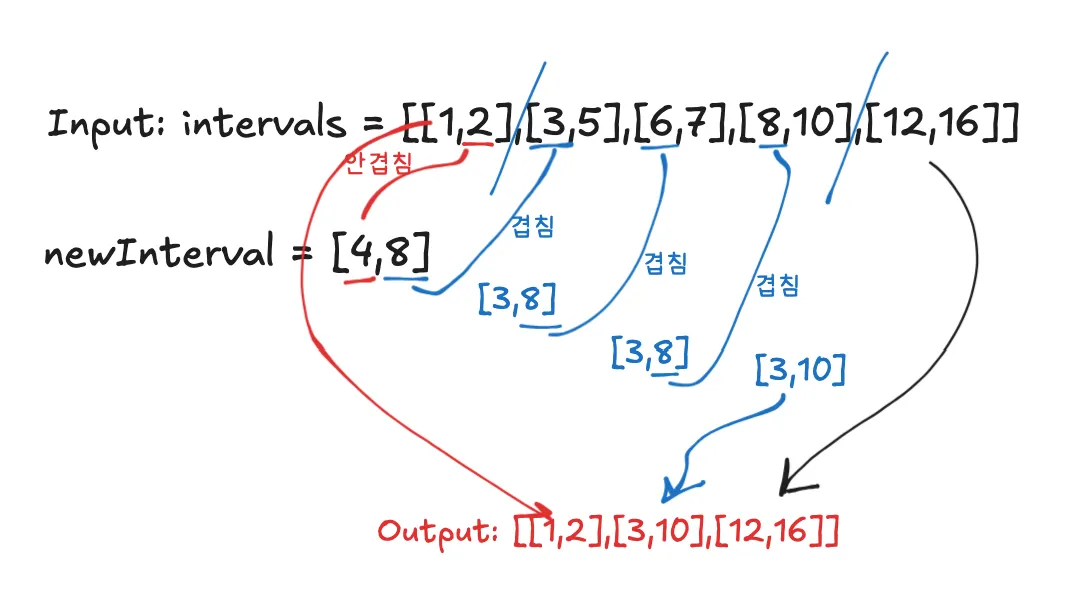
최종 결과 → [[1,2],[3,10],[12,16]]

시간 및 공간 복잡도

항목	복잡도	설명
시간 복잡도	O(n)	intervals 한 번 순회
공간 복잡도	O(n)	결과 배열 저장

 

4. 핵심 정리

개념	설명
문제 유형	Array, Interval, Greedy
핵심 아이디어	세 구간(앞쪽, 겹치는 구간, 뒤쪽)으로 나누어 처리
핵심 변수	i, newInterval, result
시간 복잡도	O(n)
공간 복잡도	O(n)
포인트	정렬된 구간 배열을 활용 → 순회 한 번으로 효율적 병합